Modelling Vitamin D from the sun in Poland – 2011
A mathematical model for seasonal variability of vitamin D due to solar radiation
Journal of Photochemistry and Photobiology B: Biology xxx (2011) xxx-xxx
J.W. Krzyscin , J. Jaroslawski, P.S. Sobolewski
Institute of Geophysics, Polish Academy of Sciences, 64 Ksiecia Janusza St., 01-452 Warsaw, Poland
Accepted 25 July 2011, Available online xxxx
Abstract
It is widely recognized that vitamin D deficiency has detrimental health consequences. The ultraviolet (UV) B radiation increases the serum vitamin D level, expressed by 25-hydroxyvitamin-D3 [25(OH)D]. An analytical model is presented to calculate the serum 25(OH)D changes throughout a year, caused by the solar exposure variability due to geophysical and habitual factors. The model is tuned by taking into account recent experimental results of serum 25(OH)D changes, after a series of artificial (by fluorescent tubes) UV exposures. The model uses the erythemal and vitamin D weighted irradiances, inferred from the Brewer spectrophotometer and the Kipp and Zonen broad-band meter measurements, carried out in Belsk (52°N, 21°E), Poland, in 2010. The modeled seasonal pattern of the serum 25(OH)D concentration in Polish indoor workers is only slightly different, than in subjects with typical outdoor activity habits, and in those with sun-seeking behavior. A deep minimum in the serum 25(OH)D concentration appears in late winter, regardless of outdoor activity habits. An extra sunbathing to boost the vitamin D level is not worth taking, because of a minor improvement of the vitamin D status, and because of a greater erythema risk. It would be much safer and more effective to maintain an adequate vitamin D level through diet supplements, even in summer, for non sun-seeking subjects.
(the following is text and some graphics extracted from PDF for translation)
1. Introduction
A skin exposure to the solar ultraviolet (UV) radiation is a basic source of vitamin D for humans [1,2]. Many recent papers demonstrated health problems related to a low level of vitamin D. It is well established that vitamin D is essential for the bone and muscle status [3,4]. It has been suggested in literature that the vitamin D insufficiency might also be related to a higher risk of colorectal cancer, prostate cancer, multiple sclerosis, type-1 diabetes, and cardiovascular diseases [5-9]. Otherwise, the increased UV exposure could induce several diseases, such as nonmelanoma skin cancers, cataracts [10], DNA damage [11], immune suppression [12], etc. Thus, balancing beneficial and harmful solar UV effects is of a special importance for health status [13].
The typical measure of the vitamin D status is a serum concentration of the 25-hydroxyvitamin D [25(OH)D]. Several studies indicated the vitamin D insufficiency across Caucasian population, based on measurements of the serum 25(OH)D levels [14-16]. The studies applied a statistical approach for finding a relationship between changes of the serum 25(OH)D level and the solar UV exposure. The vitamin D synthesis in a human body depends on a number of causes, including geographical factors (solar elevation, ozone, cloudiness, albedo, etc.), as well as on individual human factors (skin phototype, outdoor activity habits, age, genetic factors, etc.). Mathematical modeling is a promising tool to analyze the vitamin D changes, related to all these factors. Such modeling has already begun [17]. An alternative model is presented here for an estimation of the seasonal changes in serum 25(OH)D, for various scenarios of outdoor behavior. The model is constructed taking into real UV exposures, measured in Poland in 2010, and findings of recent laboratory experiments with the UV light, emitted by fluorescent tubes [18-21].
2. Methods and data
2.1. Ambient UV radiation
The surface UV radiation at the Central Geophysical Observatory of the Institute of Geophysics, Polish Academy of Sciences, in Belsk (52°N, 21°E, central Poland), has been measured by various broadband instruments since 1975, and by the Brewer spectrophotome-ter (BS) since 1992. The UV series has been recently homogenized and used for the trend detection for the period of 1976-2008 [22]. The biologically effective (BE) spectral irradiances for the erythema appearance, and production of pre-vitamin D3 from the 7-dehydrocholesterol, were obtained by using the CIE action spectra for erythema [23], and the vitamin D production [24], respectively, as the weighting functions for all of the BS spectra, collected in 2010. The ShicRIVM algorithm [25] was applied to extend the spectra from the measured 290-325 nm range, up to 400 nm.
To run our model and compare it with the previous model [17], we calculated the BE fractional daily doses for 1 h or 2 h period, on each day of 2010. Normally, there are 1-4 Brewer UV measurements, performed every hour throughout the day. Such time resolution gives only a crude approximation of 1 h doses, as clouds may affect the surface UV irradiance on much shorter time scales. Thus, the BE fractional daily doses have to be reproduced from proxy variables, correlated with the UV irradiance. The following proxies were selected: the output (in Volts) of the collocated Kipp and Zonen UV broad-band meter, the UV-S-EA-T, solar elevation from an astronomical formula, and the amount of ozone in the whole column of the atmosphere (from the nearest BS ozone measurements). A multiple regression model of the BE irradiance, measured by the BS during clear-sky conditions, on the proxy values at the time of BS measurement, was constructed. A standard least-squares procedure was applied to find the regression constants. Subsequently, the 1 min BE irradiances were calculated throughout the whole day, using a linear combination of regression constants, and the time series of the regression proxies. Similar procedures were commonly used in the past reconstructions of the ground level solar UV [26-28].
Two regression models are considered here to calculate the ery-themal and vitamin D weighted irradiances with 1 min resolution. The erythemal irradiances from the reconstruction model differ only slightly, by about 2-3% ± 7% (standard error), from the routine erythemal irradiances, detected by the Belsk broad-band meter. Moreover, the reconstructed vitamin D irradiances agree (within a ±5% range) with those derived by the recently proposed statistical model, that converts the observed erythemal irradiances (from the Belsk's UV broadband meter) to the vitamin D weighted irradi-ances with an accuracy of about 10% [29].
The BE doses are expressed in hundreds of BE Joules per square meter. The standard erythema dose (SED) of 100 Jeryt rrr2 is used as a standardized measure of erythemogenic UV radiation. The value of 100 JvitD3 m-2 also approximates the standard vitamin D dose (SDD), corresponding to the UV exposure on 25% of the whole skin area, that is equivalent of an oral daily dose of 1000 IU vitamin D, necessary to keep sufficient vitamin D level in the blood. The recent estimation of the SDD value was about 106 JvitD3 mr2 for the skin phototype II [30]. The latest calculations suggested the lower value of SDD [31]. There is no common agreement on the shape of the pre-vitamin D3 action spectrum, reflecting uncertainties of the photoconversion rate of pro-vitamin D3 to pre-vitamin D3 in human skin [32]. Hereafter, we denote 1 SDD = 100 JvitD3 mr2. However, this may only be a rough estimate of the UV exposure on 25% skin area, providing an adequate vitamin D status.
Table 1
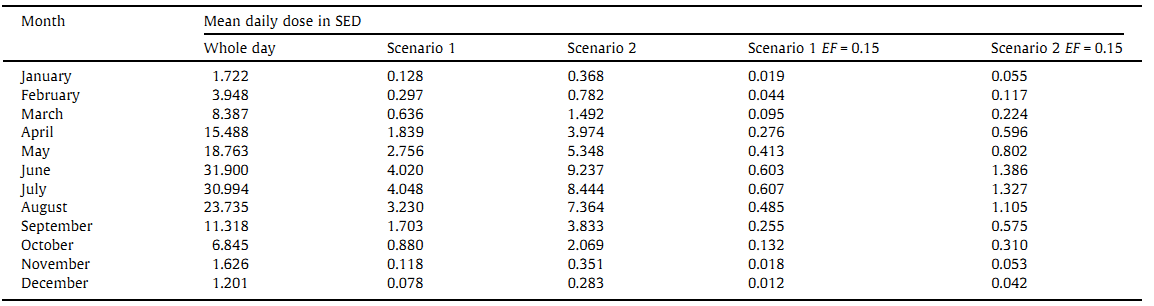
Tables 1 and 2 include the monthly means of daily and fractional BE doses, corresponding to a hypothetical behavior of Polish indoor workers. The daily UV exposure are calculated from a 1 min series of the BE irradiances. The mean ratio of the vitamin D action spectrum weighed UV, and the erythemal weighted UV, reaches the late spring/summer plateau (May-August) of 1.7-1.8, and the winter (December-January) minimum of 0.8, that corresponds to the ratios found at mid-latitudinal Canadian stations [29].
The average time spent outside, during working days, is supposed to be 1 h (7.30-8.00 am and 3.00-3.30 pm local time, during home-office-home travel). During weekends, it is 1 h around the local noon in the cold period of the year (16 October-14 April), or 2 h in the warm period of the year. This schedule corresponds to that found for British adults [14]. An alternative scenario assumes that the weekend scenario is valid also for all working days. This scenario is more appropriate for persons on maternity leaves, or for healthy pensioners.
For a standing subject in a mid-latitudinal region (latitude about 50°N), without a hat, about 10% of the whole body (including the face, neck, and hands) is normally exposed. The subject may receive between 5% and 50% of possible daily irradiation, that is incident on horizontal surfaces exposed to the direct sunlight [33]. Following the recent model [17], we assume that a subject receives 15% of the ambient dose at Belsk. Table 1 shows that for such a person, there is a minimal erythema risk during the whole year, as the monthly means of daily erythemal doses are always less than 2 SED (i.e., below the threshold to produce the skin reddening even for a subject with the skin phototype I [34]). Table 2 shows that subjects with typical and sun-seeking habits, exposing 1/4 part of the whole body, could receive the UV doses, equivalent to the oral daily intake of 1000 IU vitamin D, in the period of June-July 2010 (normal scenario), and April-September 2010 (sun-seeking scenario), respectively. Fig. 1 indicates that there was the erythema risk on some days during late spring and summer in 2010, even for subjects with the skin phototype II, receiving only 15% of the ambient UV dose, during a 2 h solar exposure around noon in the warm period of the year.
2.2. Analytical model
Following the model proposed by Diffey [17], for a description of seasonal variation of vitamin D due to the solar radiation, we define a response function R(t), which provides the serum 25(OH)D concentration t days after a single exposure of 1 SDD, i.e., R(t)=F{2-t/x - 2-t/b)(1) where F is a normalizing factor, a is the half-life (days) for the disappearance of 25(OH)D, and b is the half-life for the synthesis of
Table 1
Monthly means of daily erythemaly weighted doses from the measurements carried out in Belsk, central Poland, in 2010 for the following scenarios: the whole day insolation (from sunrise up to sunset), scenario 1 - the outdoor activity in the periods 7.30-8.00 am + 3.00-3.30 pm in working days and 1 h (cold subperiod of the year) or 2 h (warm subperiod, 15.04-15.10) around noon in weekends, scenario 2-outdoor activity 1 h and 2 h around noon in all days in cold and warm subperiod of the year, respectively. For scenario 1 and 2, the exposure fraction (EF) of 0.15 is assumed.
Month Mean daily dose in SED
Table 2
The same as Table 1 but the values represent vitamin D weighted doses.
Month Mean daily dose in SDD
Figure1
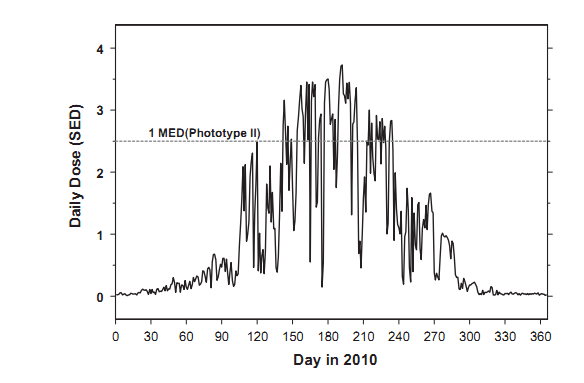
Fig. 1. Erythemally weighted fractional daily exposures based on the UV measurements at Belsk, central Poland, in 2010 for 1 h (2 h) outdoor activity symmetrical around noon in the cold (warm) subperiod of the year. A subject receives 15% of ambient exposures. The cold subperiod is for 16 October-14 April. The horizontal line shows the 1 MED threshold (2.5 SED) for the skin phototype II.
25(OH)D. Values for a and b are assigned equal to those selected in the Diffey model [17], i.e., 30 and 3 days, respectively. Diffey assumed F =13 nmol L-1 per 1 SED, based on Adam's et al. [35] indoor experiment (which shows that a single whole-body exposure, causing a minimal reddening of white skin, yields the maximum 25(OH)D increase of about 27 nmol L-1).
People are exposed to the solar UV radiation on a daily basis during outdoor life activity. Thus, the 25(OH)D concentration after day T, C(T), due to sunlight is a sum of the UV exposures (UV(t)) , received in previous days t =1.....T-1, and (UV(T)), received on day T. The exposures are weighted according to (i) a fraction of a whole body (A) open to sunlight, and (ii) an exposure fraction (EF), received by a subject (i.e., a fraction of the ambient UV radiation, incident on not shaded horizontal surfaces), and (iii) a human response to the UV radiation, as defined by the response function R. After Diffey [17], we have adopted the following general expression: C(T) = y*(UV(t)) x EF(t)xA(t)xR(T - t + 1) (2)
In the Diffey model, a value of 33 nmol L-1, due to non-solar factors, was added to C(T), in order to have the serum 25(OH)D level combining both effects, the oral intake and the solar UV exposure.
We employ a new formula for the normalizing factor in Eq. (1), based on results of a recent indoor experiment [21]. During this experiment, participants were exposed to fixed UVB doses of 0.75, 1.5, or 3 SED. They had 6%, 12%, or 24% of the whole body radiated by the fluorescent tubes TL12 (broadband UV-B). Each participant underwent four UV-B exposures at intervals of 2-3 days. The 25(OH)D levels were measured before, and 48 h after the final exposure. We focus on the results obtained for the participants with 12% of the whole body exposed four times to UVB of 0.75,1.5, or 3.0 SED. Our model takes into account the vitamin D weighted UV doses (in SDD), as the measure of the solar effectiveness in vitamin D synthesis. Thus, the experiment doses in SED need to be recalculated in SDD. The conversion constant (SED ? SDD) of 1.3 is based on the irradiance spectrum by the TL12 tube. The exposures used in the experiment correspond to 0.975, 1.95, or 3.9 SDD, respectively. Eq. (2) is used to describe the serum concentration changes in participants during the experiment, assuming that the exposures were on 1st, 3rd, 6th, and 8th day of the experiment.
Fig. 2 shows time series of the serum 25(OH)D concentration changes due to the tube irradiation, based on Eq. (2). The concentration after the 10th day should be equal to that measured in the experiment. The following normalizing F-values of 7.12, 5.41, or 3.24 nmol L-1 per SDD are found to match the experiment results, for the exposures series of 0.975,1.95, or 3.9 SDD, respectively. The concentration curves are compared with those calculated assuming that F =13 nmol L-1 per SED (as in the Diffey model), and
A(t) = 0.12.
Figure 2
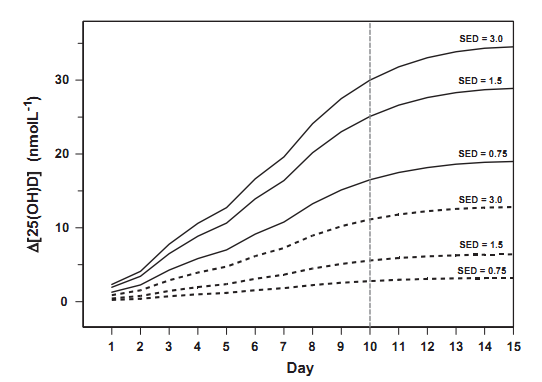
Fig. 2. Time series of the serum 25(OH)D concentration changes using the indoor experiment scenario [21]. The subjects had 12% of the whole body irradiated four times (in 1st day, 3rd, 6th, and 8th day) with 0.75,1.5, and 3.0 SED. The solid lines show the calculation with constant F =7.12, 5.41, and 3.24 nmol L-1 per SDD, respectively, to match the observed concentration at 10th day. Dashed lines represent the time series from Diffey model [17] assuming F= 13 nmol L-1 per SED for the whole body exposure.
The set of empirically derived values of F allows to construct an approximation formula, which can be used for a wide range of ambient UV exposures:
F(t) = 9.20917 exp[-0.2688EE(t)] (3) in nmolL-1 per SDD, where EE(t) = (UV(t)) EF(t) is the effective exposure (in SDD), incident on the body. Fig. 3 shows that the formula fits the experimental data quite well.
Changes of the serum 25(OH)D concentration, induced by solar exposure, were more effective for subjects having lower initial the serum 25(OH)D concentrations [36]. A rate of the concentration changes slowed down, or even came to stop, for subjects with a high serum 25(OH)D concentration [18,19,21]. Thus, the maximum concentration should exist, and further exposures will lead mostly to the production of biologically inactive photoisomers, resulting only in slight changes of the 25(OH)D concentration [37].
A new model of the seasonal 25(OH)D concentration changes needs to account for a slower rate of the 25(OH)D change with an increase of the concentration level. Thus, we assume that the serum 25(OH)D concentration after day T, C(T), which comprises both solar and diet effects, is a sum of the concentration in a previous day, C(T - 1), and the potential change of vitamin D, between day T and T - 1, due to the solar exposure, ACT,T-1, weighted by the adjustment function AD(C(t), CMIN, CMAX). The proposed model has the following form: C(T) = C(T - 1)+ ACtj-1AD(C(T), Cmin, Cmax)(4) where ACT,T-1 = C(T)-C (T - 1), C is calculated from Eq. (2), CMIN is a minimum of the 25(OH)D concentration, related to the vitamin D level due to non-solar effects (20 nmol L-1), and CMAX is the saturation level (80 nmol L-1). The last value corresponds to the 25(OH)D saturation level, discussed by Cicarma et al. [18]. Only a slight change of the 25(OH)D concentration was reported in subjects, radiated by fluorescent tubes with the initial 25(OH)D level exceeding 80 nmol L-1. The adjustment function has the following form: AD(C(t), Cmin, Cmax)= 2-/(C(t)-CMIN)/(Cmax-Cmin) (5)
An analytical form of AD, with u = 4 (Fig. 4), is arbitrarily selected. The function shape is chosen to reproduce the difference between the annual maximum and minimum of about 30-40 nmol L-1, that corresponds to the 25(OH)D annual changes, found in population studies for mid-latitudinal regions (e.g. Tasmania (male) [15], and
Figure 4
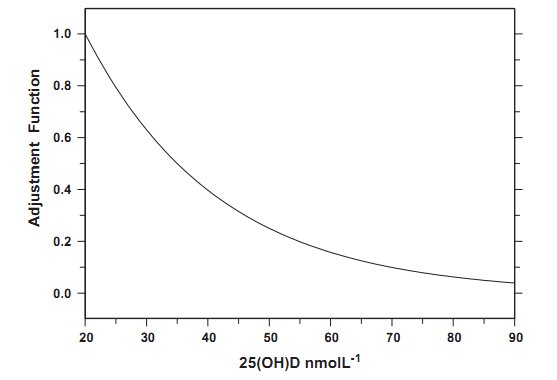
Fig. 4. The adjustment function (AD) parameterizing the photodegradation of vitamin D.
SW Germany (male and female) [38], and the maximum concentration increase after series of the UV exposures in the indoor experiments [18,21].
An iterative procedure is proposed to solve Eq. (4), for C(T) values, i.e., the values from January 1, 2010 up to December 31, 2010:
Cn(T) = Cn-1(T - 1) +ACt,t-1 AD(Cn-1(T), Cmin, Cmax)(6)
where T = 1..... 365, Co (0) = CMIN = 20 nmol L-1, the subscript n
denotes the n-th step of iteration. Iterations stop, when the absolute value of the difference Cn(T)-Cn-1(T) is less than 0.1% of Cn-1(T), that usually happens after n about 10.
For comparison purposes, we select EF(t) = 0.15 and A(t) = 0.12. It means that only the face, neck, and hands were habitually exposed. The case with A(t) = 0.24 (area of arms was added) is also examined. Recent experimental results suggested that production of vitamin D was sensitive to the area of irradiated body only for small UVB doses [21]. Thus, comparing models with A(t) = 0.12 and 0.24, we assume that the doubling of the solar forcing occurs, if the effective exposures are less than 1.95 SDD (corresponding to 1.5 SED due to TL12 tube). Such threshold is based on Bogh's et al. [21] finding of a stable level of the serum 25(OH)D, after doubling the body area, exposed to 1.5 or 3.0 SED. For a detailed discussion on the variability EF and A, see Diffey [17], and the references herein.
in
'n
"re E O
z
0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 Vitamin D weighted Dose (100 JvitD m-2)
Figure3
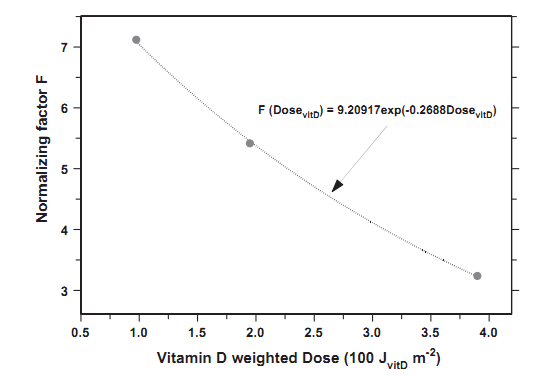
Fig. 3. F normalizing factor used in calculation of the 25(OH)D increase after single UV exposure of 12% of the whole body based on the experimental data [21] (points). Curve represents an approximation function describing the dependence of F on the effective exposures (in SDD).
3. Results
The modeled seasonal profiles of the serum 25(OH)D concentration for central Poland in 2010, and for various outdoor activity habits, are shown in Figs. 5-8. Fig. 5 depicts the outdoor activity scenario: 7.30-8.00 am + 3.00-3.30 pm, from Monday up to Friday, 1 h symmetrical around noon in the cold period of the year, on Saturday and Sunday, 16 October-14 April, and extended up to 2 h in the warm period, EF = 0.15, A = 0.12. Fig. 6 exhibits the same scenario as in Fig. 5, but the irradiated area of body was two times larger (A = 0.24) in weekends, in the warm subperiod. Fig. 7 shows the scenario as in Fig. 5, but for sun-seekers with two times larger exposure fraction, EF= 0.30, throughout the whole year. Fig. 8 displays the outdoor activity scenario: 1 h symmetrical around local noon in the cold period, and 2 h in the warm period of the year, EF = 0.15, A = 0.12 (the same constants as in Fig. 5).
The seasonal 25(OH)D profiles shown in Figs. 5-8 are obtained by both, the proposed model (Eqs. (1)-(6)), and by Diffey's model [17] (Eqs. (1) and (2), F = 13 nmol L-1 per SED). The horizontal line at 75 nmol L-1 represents the threshold for optimum bone health
Fig. 5. Modeled annual variation in the serum 25(OH)D concentration for central Poland in 2010 (dashed curve - the proposed model, solid curve - the previous model [17]) for the outdoor activity scenario: 7.30-8.00 am + 3.00-3.30 pm from Monday up to Friday; 1 h symmetrical around noon in the cold period of the year, 16 October-14 April, and 2 h in the corresponding warm period on Saturday and Sunday. The broken line at 75 nmol L-1 is the threshold for optimum bone health [39]. The exposure fraction (EF) and the irradiated part of the whole body (A) are equal to 0.15 and 0.12, respectively.
Fig. 6. The same outdoor activity scenario and exposure fraction (EF =0.15) as in Fig. 5 but the irradiated part of the whole body is doubled during weekends, A = 0.24, in the warm period of the year; 15 April-15 October. [39]. The differences in the annual pattern of 25OH(D) are mostly seen in the summer period. The annual minima in February/March agree within the range of about 5 nmol L-1. The Diffey model does not include the mechanism for the 25(OH)D saturation, that is clearly seen in Fig. 8, where the maximum concentration value reaches 110 nmol L-1, being about 25 nmol L-1 larger than that by the proposed model. Output of the proposed model is slightly influenced by changes of the outdoor activity scenario.
The proposed model provides the serum 25(OH)D concentration above the 75 nmol L-1 threshold, in two summer months (Fig. 7), for the sun-seeking indoor workers, with EF(t) = 0.30, i.e., two times larger than the assumed typical value EF(t). Both models provide 5 - month period above the threshold, for subjects being outdoors always around noon, throughout the whole year (Fig. 8). The Diffey model shows the concentration values above the threshold, from mid-June up to mid-September 2010, for the non sun-seeking indoor workers (EF(t) = 0.15), exposing a two times larger part of the body in the warm period of the year (Fig. 6). The threshold level is
Fig. 7. The same outdoor activity scenario and the irradiated part of the whole body (A = 0.12) as in Fig. 5 but the exposure fraction is doubled, EF= 0.30, for all days in
Fig. 8. The same exposure fraction, EF = 0.15, and the irradiated part of the whole body, A = 0.12, as in Fig. 5 but for subjects with different schedule of outdoor activity; 1 h symmetrical around noon in the cold period and 2 h in the warm period of the year.
never reached for the indoor workers, following typical solar habits, i.e. A(t) = 0.12, EF(t) = 0.15, and the outdoor activities around noon only during weekends (see Fig. 5 for both models, and Fig. 6 for the proposed model).
4. Discussion
The seasonal variability of the serum vitamin D levels in healthy subjects has been examined mostly using statistical tools, applied to the results of population studies [14-16]. Information how a personal behavior would affect the vitamin D status could be possible from questionnaires, asking for food habits, time, and duration of outdoor activities, clothing style, etc. However, such polls are often untrustworthy [40]. An alternative approach uses the mathematical modeling to assess how the solar exposure habits of subjects influence the vitamin D status. Diffey proposed a model of the 25(OH)D concentration changes due to the solar exposure variability, caused by seasonal changes in solar radiation and personal outdoor activity [17]. Diffey's model was calibrated using results of the experiment, carried out in the early 1980s [35].We present an extension of the Diffey model that accounts for the photodegradation of vitamin D3, and for calibration, accounting results of the recent experiments, with subjects exposed to the indoor UV radiation by fluorescent tubes [18-21].
The main differences between our and the Diffey model are listed below:
• a dietary intake leads to 20 nmol L-1 concentration of the serum 25(OH)D,
• the vitamin D weighted UV doses constitute input to the model,
• the adjustment function AD(t) is introduced to describe the vitamin D photodegradation being especially strong, with the serum 25(OH)D concentration approaching the saturation level of 80 nmol L-1,
• the normalizing factor F, in the response function R(t), depends on the effective exposure incident on the body,
• the linear dependence between the serum 25(OH)D concentration and the area of skin open to sunlight is kept, for low UV exposure, below the exposure threshold of 1.95 SDD.
In our model, the solar forcing is described in the SDD units, whereas the UV exposures in SED units were used in Diffey's model. Recent work has suggested that the vitamin D weighted doses are more appropriate, when analyzing the cutaneous synthesis of vitamin D. It means that 1-MED radiative forcing in summer has a higher potential to produce vitamin D, compared to a 1-MED source in winter. Thus, the solar exposure, expressed in MED, should be larger in winter, than that in summer, to produce the same vitamin D effect [41].
The adjustment function has an arbitrarily selected functional shape that needs further studies. At the moment, its analytical form is supported by a reasonable pattern of the annual 25(OH)D fluctuations. Our definition of the response function F(t) takes into account results of the experimental studies [21], that showed a larger response of the serum 25(OH)D concentration to a single UV exposure (see Fig. 2).
The exposure threshold of 1.95 SDD, over which the vitamin D synthesis is not affected by further increase of the exposed skin area, is based on experimental data [21], as discussed in Section 3. Holick's rule indicates that the solar exposure of 1/4 MED, over 1/ 4 of a body, is required for a sufficient vitamin D status [42,43]. Thus, it could be anticipated that a larger skin area, exposed to solar radiation, would boost the vitamin D synthesis. We repeat the calculation of the 25(OH)D seasonal pattern by our model for all cases, defined in Section 3, assuming that the vitamin D3 synthesis is always (regardless of UV intensity) proportional to the exposed skin area. The model predicts only a slight change (<1%) of the 25(OH)D seasonal values. This is because the effective exposure over the site exceeds the 1.95 SDD threshold only during short periods, when subjects have also a high level of the vitamin D serum. Thus, a further exposure increase is less effective for the vitamin D synthesis (e.g., see Table 2 data in June-July-August for scenario 2). Doubling the exposed skin area did not improve the vitamin D status in Polish indoor workers in 2010. It would be more effective in late winter and early spring (minimum serum 25(OH)D concentration), when indoor workers take a holiday in southern resorts.
Diffey's model predicted that the solar exposure, accounted for a smaller part of the overall serum 25(OH)D concentration than the commonly believed estimate by 80-90% of the vitamin D production, is due to the solar radiation [44]. Diffey's model provided that the solar UV radiation was responsible for only about 50% of the overall serum 25(OH)D concentration in British adults during winter. In our model, we assume that a dietary intake produces the 20 nmol L-1 of serum 25(OH)D concentration, and that it is also responsible for about 50% of the overall serum 25(OH)D concentration in winter for Polish indoor workers. We find about 60% and 70% contribution of the solar UV effects to the overall annual mean of 25(OH)D, respectively, for a typical (Fig. 5) and most sun-seeking (Fig. 8) behavior of a Polish indoor worker. There is a possibility to improve the vitamin D status by non-solar vitamin D sources. Various studies have shown that proper diet and vitamin D supplementation could be a basic source to keep a sufficient vitamin D status [45-47].
Seasonal changes of the serum vitamin D level in British adults, derived from Diffey's model (assuming typical British solar habits), show that the adequate vitamin D levels (>75 nmol L-1) could not be maintained throughout most of the year [17]. More outdoor activities on weekends, and exposure of larger part of skin, could significantly help to attain the adequate vitamin D level for late the spring/summer season. However, a larger erythema risk, due to the UV overexposure, has to be taken into account because of a high natural intensity of the solar UV radiation during that season [17]. An improvement of the vitamin D status, with increasing individual solar exposure, is then possible, but not recommended for the whole population, because it is not easy to keep the balance between beneficial and harmful effects of the solar UV
Our results show a similar problem for Polish indoor workers. They could not maintain the adequate vitamin D levels throughout most of the year. The results of our model showed that a sun-seeking behavior, during working days and weekends (up to 2 h outdoor activity around noon), improves the vitamin D status, but the serum 25(OH)D concentrations are only slightly above the optimum health threshold (Fig. 7). A substantial increase of vitamin D, by enlarging the exposed body surface, and/or avoiding shelters, is not possible even for sun-seeking subjects, in months with the natural high-solar radiation. A rate of the vitamin D synthesis is slowed down in that period because of an intensive vitamin D photodegra-dation, with serum 25(OH)D concentration close to its saturated value.
Diffey's model suggested that a more active outdoor activity, just only on weekends, could provide an adequate vitamin D level for almost half of the year. The results by our model are less optimistic, i.e., such a period is shortened to 2 months for the weekend sun-seekers (Fig. 7), and the adequate vitamin D level is never reached for the indoor workers with typical solar habits (Figs. 5 and 6). The UV exposures during a two months period (June-July), with the daily vitamin D weighted doses exceeding 1 SDD (Table 2, scenario 1 with EF = 0.15), could not rise the serum 25(OH)D concentration up to the threshold level for the optimum bone health (Fig. 5).
Diffey discussed that sunbathing around a midday, without applying a sunscreen in the exposed to sun environment during weekends, could have boosted the vitamin D synthesis, but was not recommended because of the erythema risk due to the UV overexposure [17]. Our model shows that the risk is not worth taking because extra exposures only slightly improve the vitamin D status. Nearly similar patterns of the serum 25(OH)D concentration are calculated for typical (Figs. 5 and 6) and sun-seeking (Fig. 7) outdoor habits, in the periods when the weather conditions permit high exposures. It would be much safer and more effective to maintain adequate vitamin D level through a diet supply. In all our scenarios, a deep minimum of the serum 25(OH)D concentration appeared in late winter. Thus, it seems that extra supplementation during the whole winter needs to be considered.
We assume that habitual factors responsible for vitamin D status, i.e. irradiated part of the whole body (A) and fraction of the daily solar radiation falling on a horizontal surface that is received during outdoor activities (EF), are constant throughout the year. We select EF = 0.15 and A = 0.12 as the reference set. The same EF and A = 0.10 were chosen by Diffey [17]. The model's sensitivity studies are carried out by doubling values of these factors and changing the outdoor activity scenarios. For a more realistic scenario, the habitual factors will be allowed to vary throughout the year due to weather variations. The factors need to be lower during bad weather (for rainy and/or cold days). Larger values are expected for sunny and warm days. Thus, the geophysical and habitual factors are somewhat correlated. Lower values than the reference values are anticipated in late autumn/winter and higher in late spring/summer, that corresponds to the minimum and maximum in seasonal pattern of the serum 25(OH)D concentration. It seems that such changes in the habitual factors do not change the overall picture of the solar radiation impact on the vitamin D status in Polish indoor workers as larger variability and larger values of the habitual factors are expected in the period when the vitamin D level is less sensitive to the UV forcing. The serum 25(OH)D concentration is high in that period that stops its further substantial increase due to intense vitamin D photodegradation.
It is worth mentioning that the proposed model provides an initial step toward modeling of the 25(OH)D changes, by focusing on the effects of specific outdoor scenarios, rather than on a complete description of factors, responsible for the vitamin D status of subjects. It seems that the model needs to account for individual subject characteristics, e.g., age, skin pigmentation, body index, sunscreens used, etc. The basic advantage of the mathematical modeling is in a prognostic aspect, when searching for more effective and save scenarios of the adequate vitamin D levels. Otherwise, the problem is difficult to solve based on results of clinical and population studies.
Acknowledgments
This work was partially supported by a Grant from the State Inspectorate for Environment Protection in Poland, under Contract No. 48/2010/F.
References
[1] M.F. Holick, Vitamin D requirement for humans of all ages: new increased requirements for women and men 50 years old and older, Osteoporos. Int. 8 (2) (1998) 24-29.
[2] M.F. Holick, Deficiency of sunlight and vitamin D, BMJ 336 (2008) 1318-1319. [3] M.C. Chapuy, M.E. Arlot, F. Duboeuf, J. Brun, B. Crouzet, S. Arnaud, P.D. Delmas, P.J. Meunier, Vitamin D and calcium to prevent hip fractures in elderly women, New Engl. J. Med. 327 (1992) 1637-1642.
[4] M.F. Holick, Sunlight 'D'ilema: risk of skin cancer or bone disease and muscle weakness, Lancet 357 (2001) 4-6.
[5] A.M. Hughes, A. Kricker, B.K. Armstrong, C.M. Vajdic, J. Turner, A.E. Grulich, L. Fritschi, S. Milliken, J. Kaldor, G. Benke, Sun exposure may protect against non-Hodgkin lymphoma: a case-control study, Int. J. Cancer 112 (2004) 865-871.
[6] E. Hypponen, E. Laara, A. Reunanen, M.R. Jarvelin, S.M. Virtanen, Intake of vitamin D and risk of type 1 diabetes: a birthcohort study, Lancet 358 (2001) 1500-1503.
[7] C.J. Luscombe, A.A. Fryer, M.E. French, S. Liu, M.F. Saxby, P.W. Jones, R.C. Strange, Exposure to ultraviolet radiation: association with susceptibility and age at presentation with prostate cancer, Lancet 358 (2001) 641-642.
[8] I.A.F. van der Mei, A.L. Ponsonby, T. Dwyer, L. Blizzard, R. Simmons, B.V. Taylor, H. Butzkueven, T. Kilpatrick, Past exposure to sun, skin phenotype, and risk of multiple sclerosis: case-control study, BMJ 327 (2003) 316-320.
[9] A. Zittermann, Vitamin D in preventive medicine: are we going the evidence? Br. J. Nutr. 89 (2003) 552-572.
[10] R. Lucas, A. McMichael, W. Smith, B. Armstrong, Solar ultraviolet radiation: Global burden of disease from solar ultraviolet radiation. Geneva: WMO 2006, Environmental Burden of Disease Series 13 (2006) p. 1-258.
[11] J.L. Ravanat, T. Douki, J. Cadet, Direct and indirect effect of UV radiation on DNA and its components, J. Photochem. Photobiol. B: Biol. 63 (2001) 88-102.
[12] S.E. Ullrich, Mechanisms underlying UV-induced immune suppression, Mutat. Res. 571 (2005) 185-205.
[13] R.L. McKenzie, J.B. Liley, L.O. Bjorn, UV radiation: balancing risks and benefits, Photochem. Photobiol. 85 (2009) 88-98. [14] E. Hypponen, C. Power, Hypovitaminosis D in British adults at age 45 y: notion wide cohort study of dietary and lifestyle predictors, Am. J. Clin. Nutr. 85 (2007) 860-868.
[15] I.A. van der Mei, A.L. Ponsonby, O. Engelsen, J.A. Pasco, J.J. McGrath, D.W. Eyles, L. Blizzard, T. Dwyer, R. Lucas, G. Jones, The high prevalence of vitamin D insufficiency across Australian populations is only partly explained by season and latitude, Environ. Health Perspect. 115 (2007) 1132-1139.
[16] D. Rucker, J.A. Allan, G.H. Fick, D.A. Hanley, Vitamin D insufficiency in a population of healthy Western Canadians, CMAJ 166 (2002) 1517-1524.
[17] B.L. Diffey, Modelling the seasonal variation of vitamin D due to sun exposure, Br. J. Dermatol. 162 (2010) 1342-1348.
[18] E. Cicarma, C. Mork, A.C. Porojnicu, A.Juzeniene, T.T. Tam, A. Dahlback,J. Moan, Influence of narrowband UVB phototherapy on vitamin D and folate status, Exp. Dermatol. 19 (2010) e67-e72.
[19] M.K.B. Bogh, A.V. Schmedes, P.A. Philipsen, E. Thieden, H.C. Wulf, Vitamin D production after UVB exposures depends on baseline vitamin D and total cholesterol but not on skin pigmentation, J. Invest. Dermatol. 130(2010)546-553.
[20] M.K.B. Bogh, A.V. Schmedes, P.A. Philipsen, E. Thieden, H.C. Wulf, Vitamin D production depends on ultraviolet-B dose but not on dose rate: a randomized controlled trial, Exp. Dermatol. 20 (2011) 14-18.
[21] M.K.B. Bogh, A.V. Schmedes, P.A. Philipsen, E. Thieden, H.C. Wulf, Interdependence between body surface area and ultraviolet B dose in vitamin D production: a randomized controlled trial, Br. J. Dermatol. 164 (2011) 163-169.
[22] J.W. Krzyscin, P.S. Sobolewski, J. Jaroslawski, J. Podgorski, B. Rajewska-Wiech, Erythemal UV observations at Belsk, Poland, in the period 1976-2008: data homogenization, Climatology Trends Acta Geophys. 59 (2011) 155-182.
[23] Commission Internationale de l'Eclairage (CIE), Erythema reference action spectrum and standard erythema dose, CIE S 007/E-1998,1998.
[24] Commission Internationale de l'Eclairage (CIE), Action spectrum for the production of previtamin D3 in human skin, CIE 174, 2006.
[25] H. Slaper, H.A.J.M. Reinen, M. Blumthaler, M. Huber, F. Kuik, Comparing ground-level spectrally resolved solar UV measurements using various instruments: a technique resolving effects of wavelength shift and slit width, Geophys. Res. Lett. 22 (1995) 2721-2724.
[26] V.E. Fioletov, L.J.B. McArthur, J.B. Kerr, D.I. Wardle, Long-term variation of UVB irradiance estimated from Brewer observations and derived from ozone and pyranometers measurements, J. Geophys. Res. 106 (2001) 23009-23028.
[27] J.W. Krzyscin, K. Eerme, M. Janouch, Long-term variations of the UV-B radiation over central Europe as derived from the reconstructed UV time series, Ann. Geophys. 22 (2004) 1473-1485.
[28] L.J.B. McArthur, V.E. Fioletov, J.B. Kerr, C.T. McElroy, D.I. Wardle, Derivation of UV-A irradiance from pyranometers measurements, J. Geophys. Res. 104 (1999) 30139-30151.
[29] V.E. Fioletov, L.J.B. MacArthur, T.W. Mathews, L. Marrett, On the relationship between erythemal and vitamin D action spectrum weighted ultraviolet radiation, J. Photochem. Photobiol. B: Biol. 95 (2009) 9-16.
[30] V.E. Fioletov, L.J.B. MacArthur, T.W. Mathews, L. Marrett, Estimated ultraviolet exposure levels for a sufficient vitamin D status in North America, J.
Photochem. Photobiol. B: Biol. 100 (2010) 57-66.
[31] J.C. Dowdy, R.M. Sayre, M.F. Holick, Holick's rule and vitamin D from sunlight,
J. Steroid. Biochem. Mol. Biol. 121 (2010) 328-330.
[32] M. Norval, L.O. Bjorn, F.R. de Gruijl, Is the action spectrum for the UV-induced production of previtamin D3 in human skin correct, Photochem. Photobiol. Sci. 9 (2010) 11-17.
[33] B.L. Diffey, in: J.L.M. Hawk (Ed.), Photodermatology, Arnold, London, 1999, pp. 5-24.
[34] T.B. Fitzpatrick, The validity and practicality of sun-reactive skin types through VI, Arch. Dermatol. 124 (1988) 869-871.
[35] J.S. Adams, T.L. Clemens, J.A. Parrish, M.F. Holick, Vitamin D synthesis and metabolism after ultraviolet irradiation of normal and vitamin D-deficient
subjects, New Engl. J. Med. 306 (1982) 722-725.
[36] E.B. Mawer, J.L. Berry, E. Sommer-Tsilenis, W. Beykirch, A. Kuhnlwein, B.T. Rohde, Ultraviolet irradiation increases serum 1, 25 dihydroxyvitamin D in vitamin D-replete adults, Mineral. Electrolyte Metab. 10 (1984) 117-121.
[37] A.R. Webb, B.R. DeCosta, M.F. Holick, Sunlight regulates the cutaneous production of vitamin D3 by causing its photodegradation, J. Clin. Endocrinol
Metab. 68 (1989) 882-887. [38] C. Meier, H.W. Woitage, K. Witte, B. Lemmer, M.J. Seibel, Supplementation with oral vitamin D3 and calcium during winter prevents seasonal bone loss: a randomized controlled open-label prospective trial, J. Bone Miner. Res. 19 (2004) 1221-1230.
[39] B. Dawson-Hughes, R.P. Heaney, M.F. Holick, P. Lips, P.J. Meunier, R. Vieth, Estimates of optimal D status, Osteoporosis Int. 16 (2005) 713-716.
[40] C.A. McCarty, Sunlight exposure assessment: can we accurately assess vitamin D exposure from sunlight questionnaires? Am. J. Clin. Nutr. 87 (2008) 1097S-1101S.
[41] A.R. Webb, O. Engelsen, Calculated ultraviolet exposure levels for a healthy vitamin D status, Photochem. Photobiol. 82 (2006) 1697-1703.
[42] M.F. Holick, Sunlight and vitamin D for bone health and prevention of autoimmune diseases, cancers, and cardiovascular disease, Am. J. Clin. Nutr. 80 (2004) 1678S-1688S.
[43] M.F. Holick, Vitamin D: importance in the prevention of cancers, type 1 diabets, heart disease and osteoporosis, Am. J. Clin. Nutr. 79 (2004) 362-367.
[44] M.F. Holick, McCollum award lecture, 1994: vitamin D-new horizons for the 21st century, Am. J. Clin. Nutr. 60 (1994) 619-630.
[45] R. Vieth, Vitamin D supplementation, 25-hydroxyvitamin D concentrations, and safety, Am. J. Clin. Nutr. 69 (1999) 842-856.
[46] K.D. Cashmann, T.R. Hill, A.J. Lucey, N. Taylor, K.M. Seamans, S. Muldowney, A.P. Fitzgerald, A. Flynn, M.S. Barnes, G. Horigan, M.P. Bonham, E.M. Duffy, J.J.
Strain, J.M. Wallace, M. Kiely, Estimation of the dietary requirement for vitamin D in healthy adults, Am. J. Clin. Nutr. 88 (2008) 1535-1542.
[47] A. Burgaz, A. Akesson, A. Oster, K. Michaelsson, A. Wolk, Associations of diet, supplement use, and ultraviolet vitamin D status in Swedish women during
winter, Am. J. Clin. Nutr. 86 (2007) 1399-1404.
